Table of Contents
What is Tensiometry/Goniometry?
Tensiometry is a technique in which an instrument called a tensiometer is used to measure the surface and interfacial tension of liquids and solid surfaces. While often used interchangeably, tensiometry and goniometry are not entirely synonymous. Tensiometry is an overarching term that refers to experiments that use one of the multiple types of tensiometer instruments that are designed to support the various methods of determining surface tension and other related measurements. Goniometry specifically refers to the use of tensiometers that are designed to measure contact angles, which will be discussed in further detail in later sections of this resource. While the goniometer category of instruments includes protractors and other manual instruments that were originally used as angle measurement tools in land surveys, modern contact angle goniometers, also known as optical tensiometers, typically feature advanced technologies that render them capable of automated contact angle measurements and characterization of other properties such as surface free energy (SFE), surface and interfacial tension, and interfacial rheology, among others. Many common tensiometry methods used to determine surface and interfacial tension employ a highly sensitive balance attached to probes such as the Du Noüy ring or Wilhelmy plate. These types of measurements are carried out using modern force tensiometry hardware, rather than optical tensiometers or goniometers.
Tensiometry and goniometry are used across many industries and fields of research, including surface science research, industrial research and development, and quality control. The applications of tensiometry are far-reaching, and include the characterization of surface properties, adhesion prediction, wettability testing, surface treatment and coating assessment, and surface cleanliness analysis, among others. Many industrial standards (ISO, ASTM, IEC, etc.) related to liquid properties such as surface and interfacial tension as well as surface properties including wettability and cleanliness can be addressed using tensiometry. The following resource provides detailed information about each standard and the tensiometry protocols approved for compliance with each organization: Standards for Tensiometers | Attension (biolinscientific.com)
What is Optical Tensiometry?
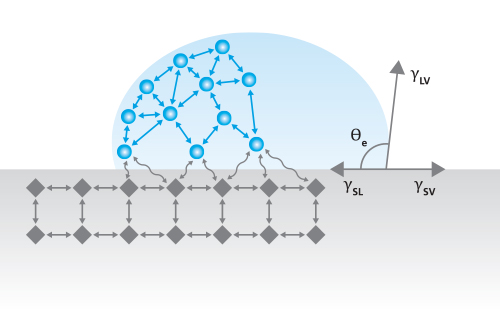
Optical Tensiometry, also referred to as contact angle goniometry, is the most common technique used to determine the contact angle of a liquid droplet on a solid and characterize its surface properties [1]. The technique relies upon the use of an optical tensiometer, also referred to as a contact angle goniometer, contact angle meter, or drop shape analyzer. In modern optical tensiometers, a liquid’s drop shape is analyzed by using a digital camera to take images of the drop. The drop image is then fit with an appropriate algorithm, usually based on the Young-Laplace equation, and a tangent line is drawn from the baseline of the droplet to its edge. The angle formed between the tangent line and the baseline is called the contact angle (θ) and can be described by the Young’s Equation (Figure 1) for an ideal surface. This straightforward measurement provides valuable information about the intermolecular forces acting at the interface between the droplet and the surface on which it sits, including surface tension and wetting properties.
The simplest measurement that can be carried out on an optical tensiometer is the sessile drop, also known as the static contact angle. In this measurement, a liquid drop is placed on a surface and the contact angle is measured as the stationary droplet sits on the surface of interest. The other primary approach used in optical tensiometry is the pendant drop method, in which the droplet is suspended from a needle or pipette tip. Additionally, optical tensiometry enables precise and dynamic measurement of contact angles during droplet advancement and recession, providing further insights into the surface chemistry and wettability of the material.
Young’s Equation:
γsv = γsl + γlvcosθγ
Besides the static contact angle, there are several other measurements that can be made using optical tensiometry, including advancing and receding contact angles, contact angle hysteresis, roll-off angle, surface free energy, surface and interfacial tension, interfacial dilatational rheology, and surface roughness-corrected contact angles. These additional techniques provide a wealth of data regarding liquid-solid interactions and enable characterization of materials in a myriad of research fields and industrial environments. For this reason, optical tensiometry is also frequently used in industrial facilities for quality control as well as standard adherence, including various ASTM and ISO standards that relate to the properties of surfaces.
Components of an Optical Tensiometer
Optical tensiometers have 4 main components:
Liquid Dispenser
Optical tensiometry measurements require a droplet to be dispensed and either deposited onto a surface, or suspended in air (e.g. pendant drop) to complete the measurements. Modern tensiometers often use pipette tips with automated, robotic dispensing systems, or syringe pumps for controlled liquid dispensing, but some lower-cost models still use manual syringes. Some tensiometers have a single liquid dispenser system, and others employ multiple liquid dispensers for easy collection of measurements such as Surface Free Energy (SFE), which requires the use of multiple probe liquids. Each type of dispenser has its benefits and drawbacks, depending on the surface being investigated and the probe liquids chosen for the measurement. A reliable, precise liquid dispenser is an important part of a contact angle experiment, as repeatability and accuracy are often critical for contact angle applications such as industrial quality control. From inconsistent drop volumes across experiments to clogged dispenser tips, a myriad of workflow inconveniences and data errors can be introduced if the liquid dispenser is not well suited for the measurement at hand.
In addition to the liquid dispenser itself, there are multiple types of dispenser attachments, including pipette tips or needles. Some measurement methods require a specific type of dispenser tip, such as a needle tip for needle-in dynamic contact angle measurements. However, in many cases, choosing the correct tip is not so straightforward. The probe liquid’s surface tension, density, and viscosity are important properties to consider, as well as chemical compatibility with the tip material. Table 1 below provides a quick guide for choosing the right dispensing tip for the probe liquids used in a particular experiment.
Selection Guide for Dispensing Tips |
|||||||
| Fluids/Tips | Stainless Steel Needle | Polypropylene (PP) Tip | PTFE Tip | (PP) Tip with Wide Orifice | Hydrophobic Needle | Parylene Coated Tip | |
| Water, diluted acid and alkali solutions | |||||||
| Low surface tension liquids e.g. Ethanol, Toluene, Acetone, Chloroform, Cyclohexane, Methanol, Acid, Adhesives, and Paints with surface tension < 30 mN/m | |||||||
| Adhesives, Coatings, and Paints with surface tension > 30mN/m | |||||||
| Diiodomethane with density > 3g/cm3 | |||||||
| High viscosity liquids e.g. Paints, Resins, and Glycerol with 100 mPa.s > viscosity > 1500 mPa.s | |||||||
| Low viscosity liquids e.g. Silicone oil, Mineral oil and Olive oil < 1 mPa.s | |||||||
| Strong acids with pH of 0 to 1 e.g. Hydrochloric acid (HCI), Sulfuric acid (H(2SO4), Nitric acid (HNO3), and Perchloric acid (HCIO4) | |||||||
| Fluoroantimonic acid (HF) with pH of -15 | |||||||
| Strong alkali with pH of 12-14, e.g. Sodium hydroxide (NaOH) or Potassium hydroxide (KOH) | |||||||
Table 1: Selection guide for dispensing tips
Another important consideration regarding the liquid dispenser is the range of drop volumes it is able to produce. Some optical tensiometry methods are volume dependent, such as the tilting method of measuring dynamic contact angle, so accurate and repeatable drop dispensing of precise volumes is critical. In other cases, the size of the sample determines how large or small the liquid drop needs to be. For samples with very small surface areas such as wires, or small dimensions such as microchips, extremely small droplets are necessary to collect a contact angle measurement. A typical contact angle measurement uses a drop that is between 1 and 10 microliters, which usually has a base diameter larger than 1 mm. If there is not enough surface area on a sample for a microliter-sized droplet, there are liquid dispensers that can precisely dispense droplets as small as 20 picoliters, which can have base diameters under 100 micrometers.
Sample Stage
Most modern optical tensiometers come equipped with sample stages that are designed with motorized movement in at least the X and Y planes, if not the Z plane as well. A motorized stage serves multiple purposes for enhancing contact angle measurements. Perhaps most important to high-volume applications such as industrial quality control, a motorized stage enables the placement of several droplets on a surface without requiring the user to physically move the stage before each drop is dispensed. In addition, most motorized stages are controlled by software programs that are able to track each drop location and ensure identical placement in repetitive tests, improving data traceability and repeatability.
In addition to XYZ movement, optical tensiometer stages will need to be tilted at times, such as in tilting dynamic contact angle measurements. Many optical tensiometers have tilting stage attachments, which use manual manipulation to adjust the tilt angle. Another common method of executing tilting measurements is by mounting the tensiometer into a tilting cradle apparatus, in which case, the stage is stationary and the entire instrument tilts.
Depending on the sample material being characterized, specialized stages can be used to mount the sample. These include large surface area stages for samples that do not fit on a standard stage, wafer mounting stages for semiconductor applications, and other customizable options for unique samples or setups.
Camera
The most important component of an optical tensiometer is its camera. This is because the baseline of the droplet is the reference point for the three-phase boundary from which contact angles are measured, and the camera’s ability to resolve the details at the baseline of the droplet will drastically affect the resulting measurement. Modern contact angle measurements use sophisticated software programs to control the camera and acquire the droplet image to fit it to the appropriate model. However, if the baseline of the droplet is incorrectly defined by the software because the low-resolution camera makes it difficult to see the minute differences between the material surface and the baseline, significant errors can be introduced, as depicted in Figure 2.
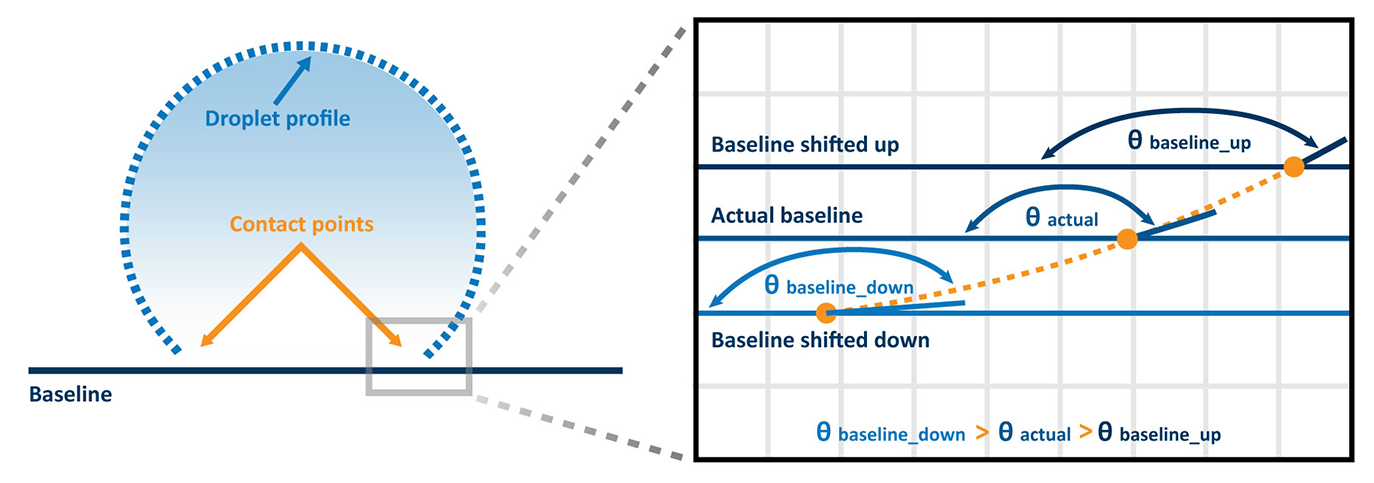
The importance of using a high-resolution camera for contact angle measurements was explored in our recent blog: Why is Camera Resolution important in Optical Tensiometry?
Besides the camera resolution, the ability to focus the camera using a manual collar or software-controlled autofocus is another important feature of an optical tensiometer. Keeping the droplet image in focus can be challenging when using manual-focus cameras, which can have similar implications regarding data quality to poor camera resolution. Some optical tensiometers have dedicated image enhancement programs built-in to their software packages in addition to autofocus capabilities, further enhancing the accuracy of their measurements.
Light Source/Backlight
Another critical component of an optical tensiometer is the light source, which is typically placed directly opposite the camera lens in the experimental setup. The illumination from the light source helps create a clean background in the image from which the contact angle is being measured. By flooding the background of the image with monochromatic light, the droplet becomes the most prominent object in the camera’s field of view. This also enhances the contrast between the drop and the surface material, improving the visibility and definition of the droplet baseline. An incorrectly identified baseline can introduce significant errors in contact angle measurements, even when the most sophisticated drop fitting algorithms are used. The most advanced optical tensiometers typically employ a monochromatic cold LED array to prevent evaporation of the sample liquid due to heat emanating from the light source and maximize image quality.
What is force tensiometry?
Force tensiometry is a technique used for measuring surface tension and interfacial tension of liquids. These direct measurements can then be used to determine dynamic contact angles, surface free energy, and adhesion force. Force tensiometry can also characterize other properties such as powder wettability, density, critical micelle concentration, and more. The key difference between optical and force tensiometry is that the force tensiometry hardware directly measures force. Force tensiometry measurements are carried out by bringing a solid sample or probe into contact with a test liquid and measuring the forces exerted on the sample by the liquid with an analytical microbalance. The size and shape of the probe, contact angle between probe and liquid, and in some cases, liquid density, are incorporated into models to relate the measured force to surface tension or interfacial tension.
Force tensiometry measurements are based on the following equation:
Wetting force = γl Pcosθ
with cosθ = contact angle, γl = surface tension of the liquid, and P = perimeter of the sample [2].
Since the inception of the force tensiometry technique, various probe attachments and experimental protocols have been developed that are now widely used for specific measurements, including the Wilhelmy plate for dynamic contact angle and surface free energy, Du Noüy ring for surface tension, Washburn vessel for powder, pigment, or fiber wettability, among others. Sample substrates can also be attached to the balance using various mounting clips with hooks to manipulate the sample in and out of the test liquid. Figure 3 below depicts one of the most common force tensiometry techniques, the dynamic contact angle measurement, using a solid sample as the Wilhelmy plate/probe.
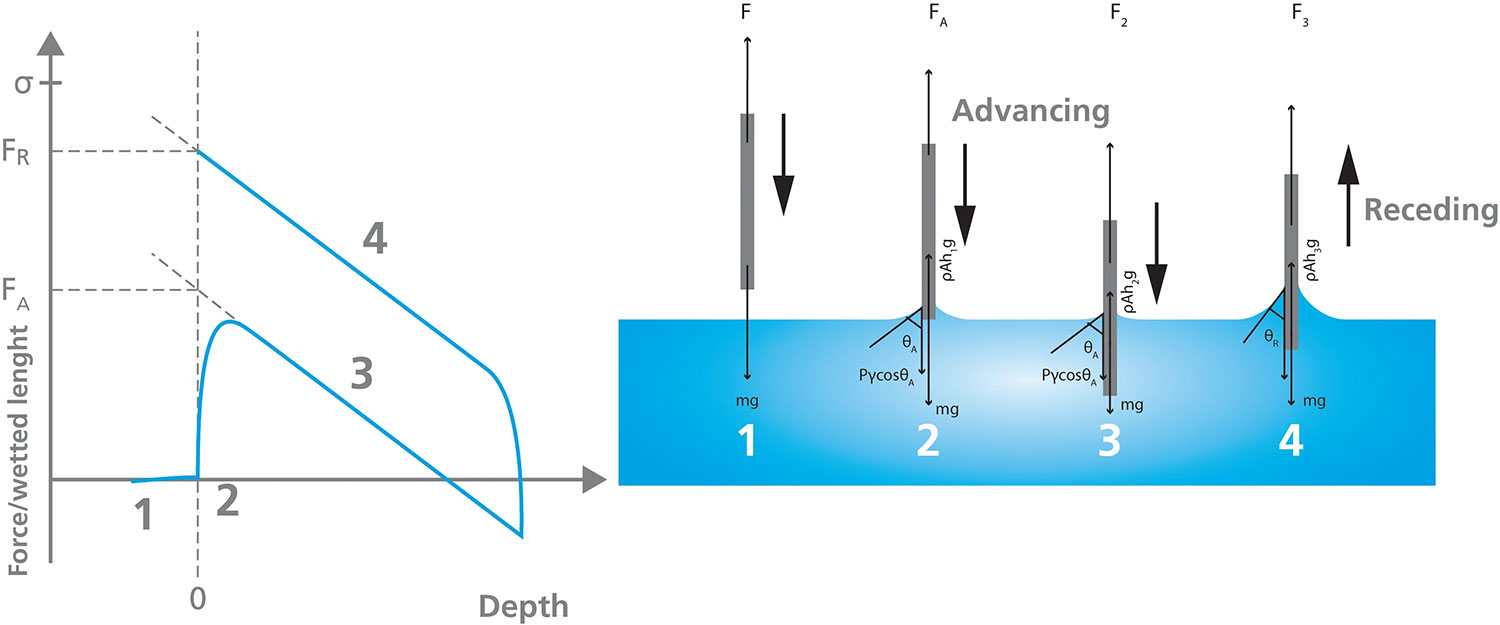
In addition to providing valuable information about the interactions between solid, liquid, and gas phases for research and development purposes, force tensiometry is frequently used to address industrial standards related to liquid characterization.
Many modern force tensiometers use automated microbalances controlled by advanced software platforms to reduce human error and streamline data acquisition and analysis. These tensiometers are capable of running experiments without user intervention and are suitable for industrial settings where many repetitions of routine measurements are necessary.
Components of a Force Tensiometer
Force tensiometers have 3 main components:
Balance
The most critical component of a force tensiometer is the balance apparatus, as the balance determines the accuracy of the measurements of forces acting on the probe or solid sample. The balance is typically housed inside the top of the instrument, with a hook at the end of the balance’s lever to attach various types of samples and measurement probes. The balance should ideally be robust enough to hold the load of a wide range of samples and probes, while maintaining extremely precise resolution in measurements of weight, force, density, and more.
Sample Stage
In most modern force tensiometers, the liquid vessel sits on a motorized sample stage, which automates the process of bringing the probe or sample into contact with the liquid and then moving them apart to collect the force measurements. The careful movement of the stage up and down throughout the measurement is vital to the accuracy of the force data, and can be accomplished with a manual stage, but is optimized through the use of an automated, motorized stage. Some force tensiometers also have built-in technology that enables the use of magnetic stirring rods on the sample stage, or thermostatic stages for experiments that require temperature control of the liquid.
Probe
Force tensiometry methods use various probes to measure forces at liquid-gas or liquid-liquid interfaces. Some probes have been specifically designed to be ideal for one type of measurement, and others are used across multiple techniques. In the following sections, we review some common force tensiometry probes and their utility for various measurement methods.
Wilhelmy plate
In the Wilhelmy Plate method, a rectangular object is used as a probe for measuring Surface Tension or Dynamic Contact Angles via force tensiometry. This technique employs a Wilhelmy Plate suspended from the tensiometer’s balance to probe the liquid surface while measuring the force of the interaction. The plate is immersed in the liquid vessel and withdrawn, resulting in the liquid forming a meniscus [3]. Assuming a known plate perimeter and a contact angle of zero degrees between the plate and liquid, the surface tension of the liquid can be quantified by analyzing the mass of the liquid pulled up by the plate. Additionally, if the surface tension of the liquid is known, this technique can also be used to measure dynamic contact angle.
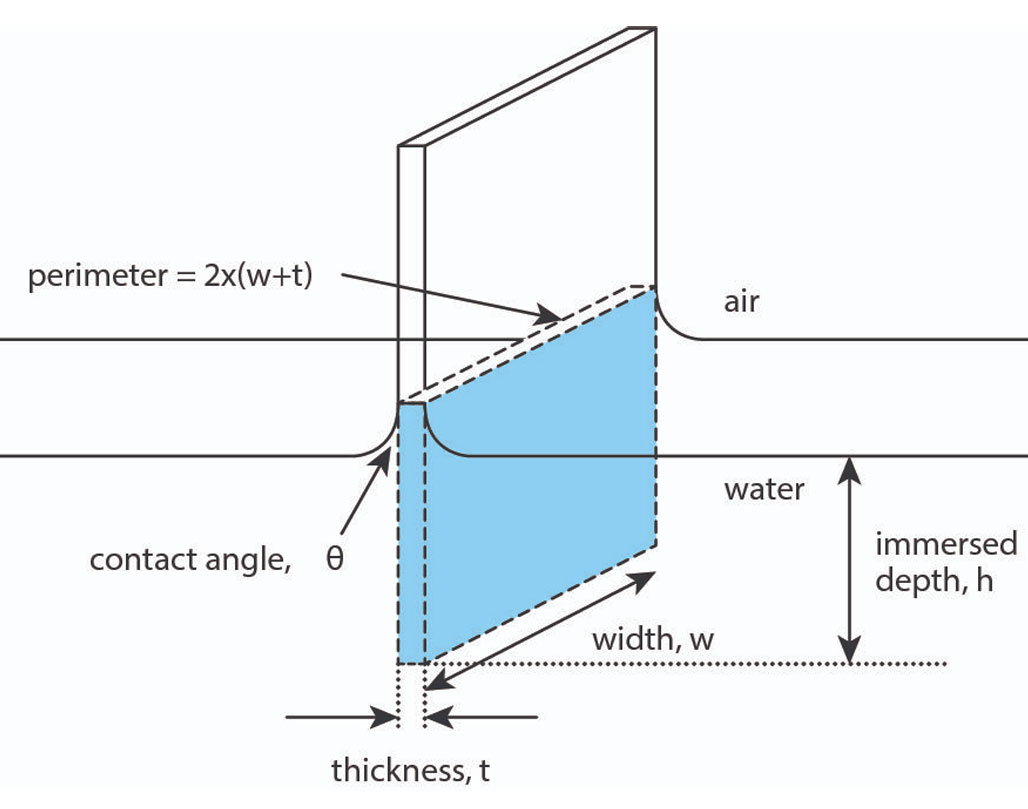
Measurements are calculated based on the part of the probe that is immersed in the liquid, represented in Figure 4, and are derived from the following equation:
F(h) = Pγ cosθ – ρAhg
Where P is the perimeter of the plate, γ is the surface tension of the liquid, θ is the contact angle between the plate and the measured liquid, ρ is the density of the liquid, A is the surface area of the plate, h is the immersion depth, and g the gravitational constant
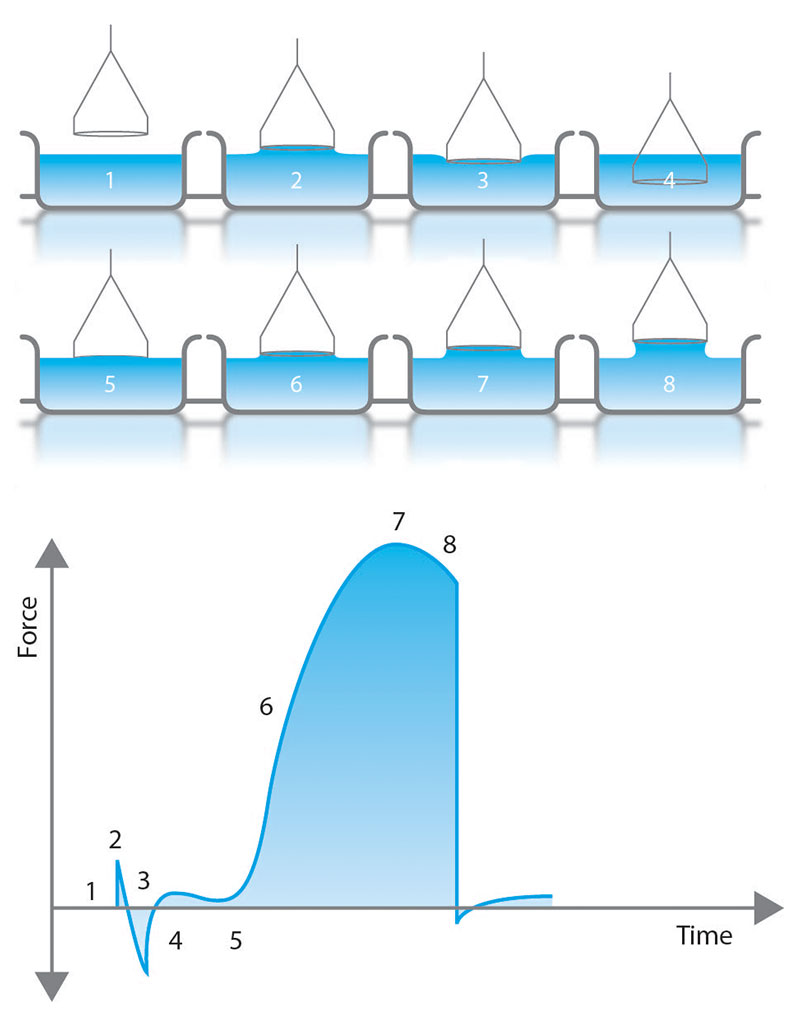
Du Noüy Ring
The Du Noüy ring is commonly used in force tensiometry for measuring the surface tension of liquids and the interfacial tension between two liquids [4] [5]. Figure 5 provides an overview of a typical Du Noüy ring measurement. The first stage of the experiment involves immersing the platinum ring in the liquid vessel and lowering the stage until the ring emerges from the liquid, surrounded by a meniscus. Just before the meniscus tears away from the ring, the volume of liquid on and around the ring is at its peak, which is also when the forces acting on the ring are at a maximum. This maximum force measurement is then used to calculate the surface and interfacial tension in each measurement.
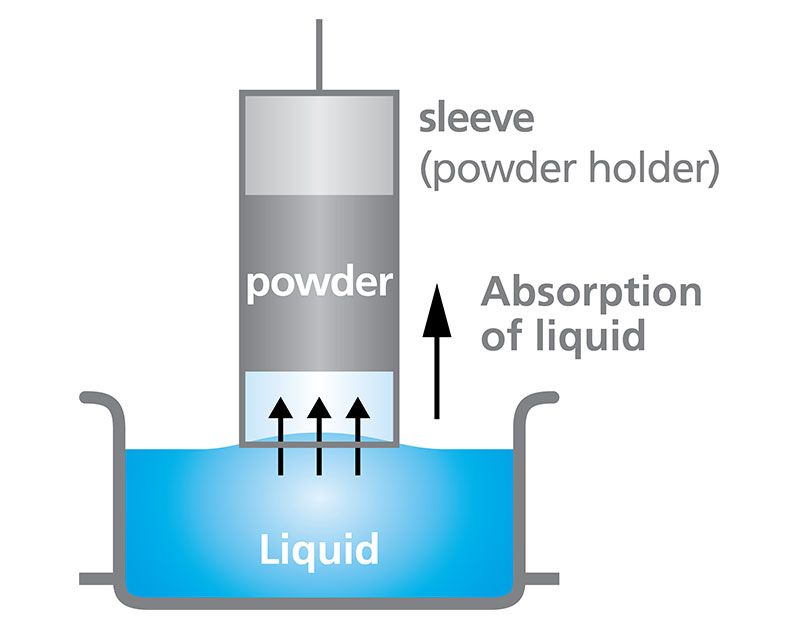
Powder Wettability Vessel (Washburn)
The Washburn method enables the measurement of powder wettability using a force tensiometer by evaluating liquid absorption into the powder over time [6]. Setting up the experiment requires the powder to be packed into a holder, depicted in Figure 6, which is typically composed of glass or stainless steel.
The holder is brought into contact with the surface of a liquid, at which point, the balance is zeroed out and left to measure the mass of liquid penetrating the powder. It is important to note that the powder wettability vessel is only suitable for powders which are known to be hydrophilic. If the powder is hydrophobic, the capillary action that typically drives the liquid to penetrate the powder container will not occur, and the measurement will be unsuccessful.
The data collected is then used to solve the Washburn Equation for the contact angle (θ):
m2 |
= |
C |
ρ2γlcosθ |
t |
||
η |
||||||
m is the measured mass, C is material constant, ρ is the density of the liquid, γl is the surface tension of the liquid, η viscosity of the liquid, t measured time, and θ contact angle
Adhesion force probe
Adhesion force refers to the force that is required to detach a liquid droplet from a surface. It is measured using force tensiometry by attaching a liquid droplet to a Pt-Ir probe on a force tensiometer, putting the drop in contact with the sample surface, and slowly separating the droplet from the surface. The resulting force-displacement curve from the measured data will clearly show the point at which the droplet separates from the surface (the pull-off force), which is the measured adhesion force. Technically, under the correct given conditions, this measurement is equivalent to the receding contact angle, since the receding contact angle is also the critical point at which the solid-liquid-gas contact point begins to retract from the surface.
Density probe
Density probes are designed specifically for determining the density of a liquid via force tensiometry. Probes for liquid density measurements are commonly made of glass and have a known weight, which are both critical variables for calculating the liquid’s density. A typical experiment is simple, the probe is lowered towards the liquid’s surface until it is fully immersed. Using the changes to the mass of the probe due to buoyancy, as well as the forces acting on the probe in the liquid allows the calculation of the liquid’s density. It is also possible to determine the density of a solid object using this method. In this case, the solid object is used as the probe and the liquid’s density must be known.
Sedimentation probe
Sedimentation in a suspension can be measured using force tensiometry by employing a sedimentation collecting probe. After fully mixing a liquid suspension, the sedimentation probe is lowered into the liquid and neither the sample stage nor the probe is moved for the duration of the experiment. Over time, particulate material from the suspension will begin to settle on the sedimentation probe, and the mass of sediment collected is measured by the tensiometer’s microbalance to determine the sedimentation rate.
What measurements can be made using a tensiometer?
Contact Angle is the most common method of quantifying the wettability of a solid and characterizing other surface properties. The contact angle is defined as the angle formed by a droplet of liquid at the point where the three phases (solid, liquid, and gas) meet, also called the three-phase boundary point. At this boundary point, there is equilibrium between the forces acting on it from the solid, liquid, and gas, or in some cases, solid, liquid, and liquid. Typically, a measured contact angle lower than 90° corresponds to high wettability, and a contact angle over 90° corresponds to low wettability [7].
An important application of the contact angle measurement is determining the surface free energy (SFE) of a solid surface. SFE is an analogous measurement to the surface tension of a liquid, with SFE and surface tension measured in mN/m, or the equivalent, dynes/cm. Although the contact angle alone provides a quantitative value that represents the wetting characteristics of the surface material, it is dependent upon the properties of the probe liquid used. SFE measurements employ multiple probe liquids for multiple measurements across a sample, followed by calculations to fit the data to one of the many theoretical models that are accepted and widely used currently [8].
Surface and interfacial tension can be interpreted in two ways: as a tension force acting along all directions of the surface per unit length, or as the energy required to increase the surface area. In both interpretations, the surface wants to minimize its surface area or potential energy. Therefore, a surface with no (or negligible) external forces will form a sphere which has the smallest surface area to volume ratio. Techniques to measure surface and interfacial tension fall into two main categories: force tensiometry where the force the surface imparts on a probe is directly measured; and optical tensiometry where the profile of a drop or bubble extracted from an image is fit to a theoretical equation.
Many products have surfactants added to their formulations to decrease the surface tension of the mixture. Surfactants are amphiphilic molecules, meaning they have both hydrophobic and hydrophilic parts, and exhibit certain molecular orientations at air-water interfaces. When these molecules are introduced to water, the hydrophilic ‘head’ of the molecule remains in the water while the hydrophobic ‘tails’ are out of the water, in air. If surfactant is added to formulations at higher and higher concentrations, eventually the surface will reach a saturation point and the surfactant molecules will begin to form micelles. This is called the Critical Micelle Concentration (CMC) and is quantified via force tensiometry by measuring surface tension as a function of surfactant concentration.
References
[1] Lander, L. M., Siewierski, L. M., Britain, W. J., & Vogler, E. A. (1993). A Systematic Comparison of Contact Angle Methods. Langmuir, 9(8), 2237-2239. https://doi.org/10.1021/la00032a055
[2] Vuckovac, M., Latikka, M., Liu, K., Huhtamäki, T., & Ras, R. H. A. (2019). Uncertainties in contact angle goniometry. Soft Matter, 15(35), 7089–7096. https://doi.org/10.1039/c9sm01221d
[3] A.W Neumann, R.J. Good, R.R. Stromberg. Surface and Colloid Science, Vol. 11, pp. 31-91. Plenum Press, New York, NY (1979).
[4] P.L. du Noüy. A new apparatus for measuring surface tension. J. Gen. Physiol 1 (1919) p. 521-524.
[5] H.H. Zuidema, G.W. Waters. Ring method for the determination of interfacial tension. Ind. Eng. Chem., Anal. Ed. 13 (1941) p. 312-313.
[6] Washburn E.W, “The dynamics of capillary flow”, The American Physical Society, Vol. XVII No.3, 374- 375.
[7] Bracco, G., & Holst, B. (2013). Surface science techniques. Springer.
[8] F.M. Fowkes. Attractive forces at interfaces. Ind. Eng. Chem. 56 (1964) 40–52.